Question

Give the domain of the following rational function using (a) set-builder notation and (b) interval notation.f(y) = y —— y-1 ——————————————————(a) Select the correct choice below and, if necessary, fill in the answer box to complete your choice.A. The domain of the given function is {yly is a real number, y # ____}(Type an integer or a simplified fraction. Use a comma to separate answers as needed.)B. The domain of the given function is {yly is a real number).

Answer 1

(a)

A. The domain of the given function is {yly is a real number, y ≠ 1}

(b)

`\begin{equation*} D=\left(-\infty\:,\:1\right)\cup\left(1,\:\infty\:\right) \end{equation*}`

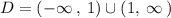
Explanation:

We have the following function:

`f(y)=(y)/(y-1)`

The domain of a function, are the input values of the function, in this case, it corresponds to the values that y can take.

Since it is a rational function and it cannot take values that make the denominator zero, so we set the denominator equal to zero, like this:

`\begin{gathered} y-1=0 \\ \\ y\\e1 \end{gathered}`

(a)

That means that y can take the value of all reals except 1.

So the correct answer is:

A. The domain of the given function is {yly is a real number, y ≠ 1}

(b)

In its interval form it would be:

`D=\left(-\infty\:,\:1\right)\cup\left(1,\:\infty\:\right)`