Question

The shorter sides of a rectangle measure 4 inches eachand one of its diagonals measures 8 inches. Which ofthe following is the measure of one of its longer sides?

Answer 1

Lets draw a picture of the rectangle:

From our figure, we can note that triangle ABC is a right triangle, so we can apply Pythagorean theorem, that is

`4^2+x^2=8^2`

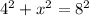
which gives

`16+x^2=64`

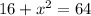
If we move 16 to the right hand side, we get

`\begin{gathered} x^2=64-16 \\ x^2=48 \end{gathered}`

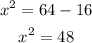
Then, x is given by

`x=\sqrt[]{48}`

since 48 = 16 x 3, we get

`\begin{gathered} x=\sqrt[]{16*3} \\ x=\sqrt[]{16}*\sqrt[]{3} \\ x=4\sqrt[]{3} \end{gathered}`

therefore, the answer is

`x=4\sqrt[]{3}`

which is the measure of the longer side.