To find:
To determine whether the x = pi/2 is the answer of the equation
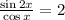
Solution:
The solution of the equation is as follows:

But at x = pi/2, the denominator of the function is zero, so, the function is not defined at x = pi/2.
Thus, the answer is "The function is not defined at x = pi/2. So, it is not the answer to the equation."