Question

I need help answering this question and the solution set

Answer 1

Let's first try to rewrite the expression to see if we can write it in a fomr more familiar:

`\begin{gathered} x-√(10-3x)=0, \\ x=√(10-3x), \\ x^2=10-3x, \\ x^2+3x-10=0. \end{gathered}`

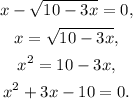
This is the same equation, but now we recognize a quadratic expression equal to 0. We can use the quadratic formula to find the solutions of this equation:

`x_(1,2)=(-3\pm√(3^2-4\cdot1\cdot(-10)))/(2\cdot1)`

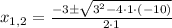
And solve:

`\begin{gathered} x_(1,2)=(-3\pm√(9+40))/(2)=(-3\pm7)/(2) \\ x_1=(-3+7)/(2)=(4)/(2)=2 \\ x_2=(-3-7)/(2)=(-10)/(2)=-5 \end{gathered}`

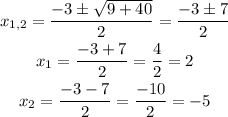
Thus, the solution set of the equation is x = -5, x = 2