Question

For the data shown, answer the questions. Round to 2 decimal places. 5.2 18.8 5.7 5 14.9 4.4 Find the mean : Find the median : Find the standard deviation :

Answer 1

Median:

1. Order the data from less to greater:

4.4

5

5.2

5.7

14.9

18.8

2. As it is a even number of data you take the average of the two data in the middle to find the median:

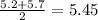
`(5.2+5.7)/(2)=5.45`The median is 5.45

Standard deviation formula (for a sample):

`s=\sqrt{\frac{\Sigma(x_i-\bar{x})\placeholder{⬚}^2}{n-1}}`

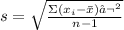
To find the standard deviation of the given data:

1. Find the difference between each data and the mean:

`\begin{gathered} (x_i-\bar{x}) \\ \\ 5.2-9=-3.8 \\ 18.8-9=9.8 \\ 5.7-9=-3.3 \\ 5-9=-4 \\ 14.9-9=5.9 \\ 4.4-9=-4.6 \end{gathered}`

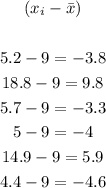
2. Find the square of each difference:

`\begin{gathered} (x_i-\bar{x})\placeholder{⬚}^2 \\ \\ (-3.8)\placeholder{⬚}^2=14.44 \\ (9.8)\placeholder{⬚}^2=96.04 \\ (-3.3)\placeholder{⬚}^2=10.89 \\ (-4)\placeholder{⬚}^2=16 \\ (5.9)\placeholder{⬚}^2=34.81 \\ (-4.6)\placeholder{⬚}^2=21.16 \end{gathered}`

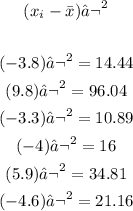
3. Find the sum of the squares:

`\begin{gathered} \Sigma(x_i-\bar{x})\placeholder{⬚}^2 \\ \\ 14.44+96.04+10.89+16+34.81+21.16=193.34 \end{gathered}`

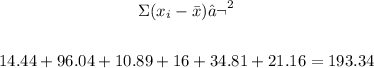
4. Use the formula of the standard deviation for n=6:

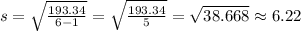
`s=\sqrt{(193.34)/(6-1)}=\sqrt{(193.34)/(5)}=√(38.668)\approx6.22`Then, the standard deviation is 6.22