Question

What is the decimal form of 100/3 100/5 and 100/6? determine whether each repeats or terminates

Answer 1

what is the decimal form of 100/3 100/5 and 100/6? determine whether each repeats or terminates ​

to know the decimal form, just make the division

Step 1

`\begin{gathered} (100)/(3) \\ (100)/(3)=100\text{ divide by 3} \\ \text{operate} \\ 100\text{ divide by 3 = 33 and 1 to left} \\ \end{gathered}`

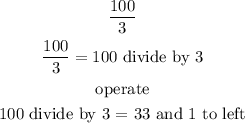
every time you divide you will have a residual number (1),

so

100=(33*3)+1

when you divide the 1 by 3, you will have

1=(3*0.3)+0.1

and

10=3*3 +1

,so the 3 will repeat forever

Step 2

`\begin{gathered} (100)/(5)=20 \\ \end{gathered}`

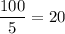
so the decimal form of 100/5 is 20

Step 3

`(100)/(6)`
`(100)/(6)=16.66`

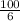
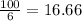
when you divide 100 by 6 you have

`\begin{gathered} 100=(16\cdot6)+4 \\ 100=96+4 \\ 16\text{.} \\ \text{and} \\ (4)/(6)=0.666 \\ so\text{ , the answer is } \\ (4)/(6)+16=16.6666 \\ \end{gathered}`

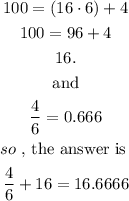
I hope it helps you.