We are required to find the value of the cosine of pi over 3.
The cosine of an angle is a ratio of the side adjacent to the angle to the hypothenuse side
Our approach is to first plot a triangle that will help us give values to this side and get our ratio.
Fortunately, pi over 3 is a special angle as we will see.
We can convert it to degrees via the formula:
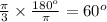
Recall that the sum of angles in an equilateral triangle of sides' ratio 2:2:2 is 180 degrees and each angle is 60 degrees.
We can find side o through Pythagoras Theorem as:
![o=\sqrt[]{2^2-1^2}=\sqrt[]{4-1}=\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/8ypolrrsebzk5py5tkl98t5r3gx50c99r1.png)
The cosine of the angle is a ratio of the adjacent side, o and hypothenuse, 2.
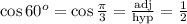
OPTION B