Answer:
![y=(1)/(2)(x-4)^2+13\text{ }\operatorname{\Rightarrow}(A)]()
Step-by-step explanation: We have to find the vertex form of the parabola equation from the given standard form of it:
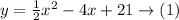
The general form of the vertex parabola equation is as follows:
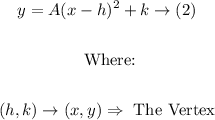
Comparing the equation (2) with the original equation (1) by looking at the graph of (1) gives the following:
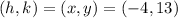
Therefore the vertex form of the equation is as follows:
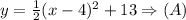
Therefore the answer is Option(A).