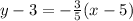Question

Use the given conditions to write an equation for the line in point-slope form and in slope-intercept form.Passing through (5,3) with x-intercept 6Write an equation for the line in point-slope form.

Answer 1

In general, the equations of a line in point-slope form and slope-intercept form are:

`\begin{gathered} y-y_1=m(x-x_1) \\ y=mx+b \end{gathered}`

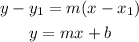
respectively. Where m is the slope of the line, b is a constant, and (x_1, y_1) is a point on the line.

Thus, the point-slope form of the line described by the problem is:

`y-3=m(x-5)`

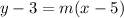
We simply need to calculate the slope of the line. For that, we simply require 2 points, we already have (5, 3) and, since the x-intercept is 6, we can deduce that the line goes through (0,6).

Therefore, the slope is:

`m=(y_2-y_1)/(x_2-x_1)=(6-3)/(0-5)=-(3)/(5)`

Then, the solution is:

`y-3=-(3)/(5)(x-5)`