Given the set of data:
11, 7, 14, 2, 8, 13, 3, 6, 10, 3, 8, 4, 8, 4, 7
Let's find the standard deviation.
To find the standard deviation, apply the formula:
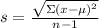
Where:
x is the data
u is the mean
n is the number of data = 15
To find the mean, we have:
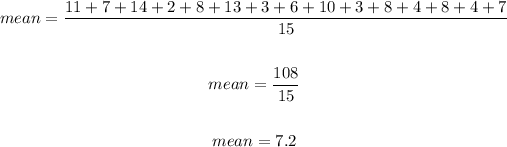
Hence, to find the standard deviation, we have:
![\begin{gathered} s=\sqrt{((11-7.2)^2+(7-7.2)^2+(14-7.2)^2+(2-7.2)^2+(8-7.2)^2+(13-7.2)^2+(3-7.2)^2+(6-7.2)^2+(10-7.2)^2+(3-7.2)^2+(8-7.2)^2+(4-7.2)^2+(8-7.2)^2+(4-7.2)^2+(7-7.2)^2)/(15-1)} \\ \\ s=\sqrt{(188.4)/(14)} \\ \\ s=√(13.457) \\ \\ s=3.7 \end{gathered}]()
Therefore, the standard deviation is 3.7
xzANSWER:
3.7