Question

What is the equation of the circle whose diameter is the segment with endpoints (4,3) and (20,-9).

Answer 1

`(x-12)^2+(y+3)=100`

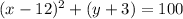
Explanations:

The standard equation of a circle is expressed according to the equation

`(x-a)^2+(y-b)^2=r^2`

where;

(a, b) is the coordinate of the centre of the circle

r is the radius of the circle;

Get the diameter of the circle;

`\begin{gathered} D=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ D=\sqrt[]{(20-4)^2+(-9-3)^2} \\ D=\sqrt[]{16^2+(-12)^2} \\ D=\sqrt[]{256+144} \\ D=\sqrt[]{400} \\ D=20\text{units} \end{gathered}`

For the radius of the circle;

`\begin{gathered} r=(D)/(2) \\ r=(20)/(2) \\ r=10\text{units} \end{gathered}`

Get the centre of the circle. Note that the centre will be the midpoint of the given endpoints as shown;

`\begin{gathered} (a,b)=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ (a,b)=((4+20)/(2),(3-9)/(2)) \\ (a,b)=((24)/(2),-(6)/(2)) \\ (a,b)=(12,-3) \end{gathered}`

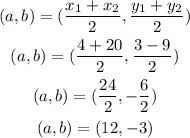
Substitute the centre (12, 3) and the radius 10 units into the equation of the circle above to have:

`\begin{gathered} (x-12)^2+(y-(-3))^2=10^2 \\ (x-12)^2+(y+3)=100 \end{gathered}`

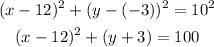
This gives the equation of the circle whose diameter is the segment with endpoints (4,3) and (20,-9).