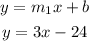Given:
The equation of line is,

As given that the required line is perpendicular to the above line.
It means the slope of required line will be negative reciprocal of above line.
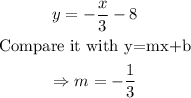
The slope of the required line will be,
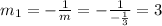
Now, given that the required line passing through point (7,-3) .
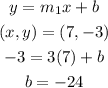
The slope-intercept form is,