Question

48 feet wide . the sides of the roof meet to form a right angle and both sides of the roof are the same length. find the length of the roof rafters find x

Answer 1

Given the image in the question, it can be seen that the roof forms a right angled triangle. Therefore, we can get the length of the roof rafters (x) by using the Pythagoras theorem.

Step 1: We define the Pythagoras theorem and state our parameters

`\begin{gathered} \text{hypotenuse}^2=opposite^2+adjacent^2 \\ \text{hypotenuse}=48ft,\text{ adjacent=opposite=}xft \end{gathered}`

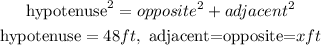
Step 2: We substitute the values into the theorem to solve for x

`\begin{gathered} 48^2=x^2+x^2 \\ 2x^2=2304 \\ x^2=(2304)/(2) \\ x^2=1152 \\ x=\sqrt[2]{1152} \\ x=33.9411255 \\ x\approx33.94ft \end{gathered}`

Hence, the length of the roof rafters (x) is 33.94ft to the nearest hundredth.