Question

If raindrops are falling vertically at 7.90 m/s, what angle from the vertical do they make for a person jogging at 2.47 m/s? (Enter your answer in degrees.)

Answer 1

17.36 degrees

Step-by-step explanation

Step 1

Diagram:

so, we have a rigth triangle then let

`\begin{gathered} angle\text{ =}\theta \\ opposite\text{ side= 2.47} \\ adjacent\text{ side =7.9} \end{gathered}`

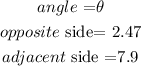
Step 2

now, we need a function that relates those values to find the missin angle , it is

`tan\theta=\frac{opposite\text{ side}}{adjacent\text{ side}}`

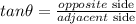
replace ans solve for the angle

`\begin{gathered} tan\theta=(2.47)/(7.9) \\ tan\theta=0.31 \\ inverse\text{ tan function in both sides} \\ \tan^(-1)(tan\theta)=\tan^(-1)(0.31) \\ \theta=17.36\text{ \degree} \end{gathered}`

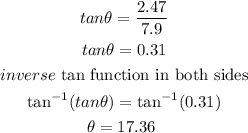
therefore, the answer is

17.36 degrees

I hope this helps you