The Solution:
Part (a)
Representing the problem fully in a diagram, we have:
Part (b)
We are required to find the length of QA= x.
We shall use Trigonometrical Ratio as below:

Making x the subject of the formula, we get
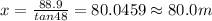
Thus, the distance from the control tower to point A is 80.0 meters.
Part (c)
We are required to find the length of AB= y.
Considering triangle PQB, we have:
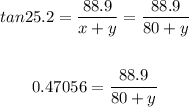
Solving for y, we get
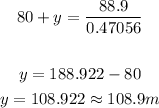
Thus, the distance moved by the plane from its initial position is 108.9 meters.