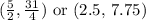To use completing the square to find the vertex of the given parabola, we proceed as follows:
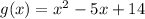
- we divide the coefficient of x by 2 and add and subtract the square of the result, as follows:
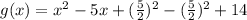
- simplify the expression as follows:
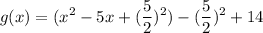
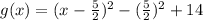
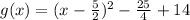

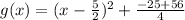
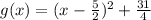
From the general vertex equation, given as:

The coordinate of the vertex is taken as: (h, k)
Therefore, given:
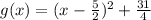
We have the vertex to be: