Given two points, the equation of the line in slope form can be obtained using this equation
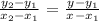
Now we can name the points
x1 = 2, y1 = 8
x2 = 4 , y2 =9
These coordinates can then be substituted into the equation
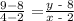
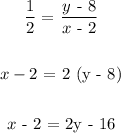
x - 2 + 16 = 2y
2y = x - 2 +16
2y = x + 14
Divide both sides by 2
y = x/2 + 14/2
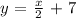
This is the equation in slope-intercept form
where the slope = 1/2