Question

5. What is the sum of 3 5/24, 6 7/24, and 9 9/24?,A. 14²/3B. 14 1/8C. 18 7/8D. 13 1/2

Answer 1

To answer this question, we can realize that we have mixed fractions. Then we need to add integers and fractions separately as follows:

1. We have:

`3(5)/(24)+6(7)/(24)+9(9)/(24)`

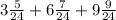
2. And this expression is equivalent to:

`3+(5)/(24)+6+(7)/(24)+9+(9)/(24)`

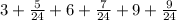
3. Now, we can add the integer parts, and the fractional parts separately as follows:

`(3+6+9)+((5)/(24)+(7)/(24)+(9)/(24))`

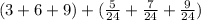
4. Therefore:

`18+(5+7+9)/(24)=18+(21)/(24)`

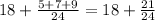
5. We finally need to simplify the fraction, and then we will have:

`\begin{gathered} (21)/(24)=((21)/(3))/((24)/(3))=(7)/(8) \\ 18+(7)/(8)=18(7)/(8) \end{gathered}`

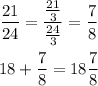
In summary, therefore, we have that the sum of the above fractions is:

`18(7)/(8)`

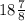
[Option C.]