Question

Create a table of values for the function and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result. (Round your answers to four decimal places. If an answer does not exist, enter DNE.)

Answer 1

Explanations:

Given the limit of the function expressed as:

`\begin{gathered} \lim _(n\to0)(\sin8x)/(x) \\ f(x)=(\sin 8x)/(x) \end{gathered}`

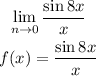
First, we need to create a table for the given values in the table:

If x = -0.1

`\begin{gathered} f(-0.1)=(\sin8(-0.1))/(-0.1) \\ f(-0.1)=(\sin(-0.8))/(-0.1) \\ f(-0.1)=0.1396 \end{gathered}`

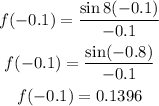
If x = -0.01

`\begin{gathered} f(-0.01)=(\sin8(-0.01))/(-0.01) \\ f(-0.01)=(\sin(-0.08))/(-0.01) \\ f(-0.01)=0.1396 \end{gathered}`

If x = -0.001

`\begin{gathered} f(-0.001)=(\sin8(-0.001))/(-0.001) \\ f(-0.001)=(\sin(-0.008))/(-0.008) \\ f(-0.001)=0.1396 \end{gathered}`

From the values above, we can conclude that the values of f(x) will all tend to be 0.1396 for the positives values of x

Therefore, we can conclude that as you approach the value 0 from the positive and negative directions, they approach the same value, hence the limit does exist.