Answer:
The escape velocity = 9.66 km/s
Step-by-step explanation:
The mass of the planet is represented by m
![m=4.9*10^(24)\operatorname{kg}]()
The radius is represented by r
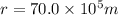
The gravitational constant is represented by G
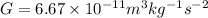
The escape velocity (v) is given by the formula:
![\begin{gathered} v=\sqrt[]{(2GM)/(r)} \\ v=\sqrt[]{(2*6.67*10^(-11)*4.9*10^(24))/(70*10^5)} \\ v=\sqrt[]{(65.366*10^(13))/(70*10^5)} \\ v=\sqrt[]{0.9338*10^8} \\ v=\sqrt[]{93380000} \\ v=9663.33\text{ m/s} \\ v=9.66\text{ km/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/uw011sutut6g6v7jz6rzfec9fvtc2m7e79.png)
The escape velocity = 9.66 km/s