Question

Consider the right triangle with leg lengths of 5 and 12 units shown in the image below. One vertex of the triangle is located at (-6, 4).

Answer 1

Step 1

Define the equation of a circle

`\text{The equation of a circle = (x-h)}^2+(y-k)^2=r^2`

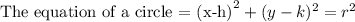
Step 2

Write down the parameters

r = radius = ?

h = -6

k = 4

Step 3

find the radius

Considering the triangle we can find the radius using the Pythagoras theorem

`r^2=5^2+12^2`
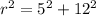
`\begin{gathered} r\text{ = }\sqrt[\square]{25\text{ + 144}} \\ r\text{ = }\sqrt[]{169} \\ r\text{ = 13} \end{gathered}`

Step 3

Substitute the values into the equation and simplify

`\begin{gathered} (x-(-6))^2+(y-4)^2=13^2 \\ (x+6)^2+(y-4)^2=13^2 \end{gathered}`

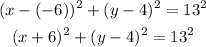
Answer is option A