Question

Hans cell phone plan cost $200 to start, then there is a $50 charge each month.a. what is the total cost ( start-up fee and monthly charge) to use the cell phone plan for one month? b. what is the total cost for x months?c. graph the cost of the cell phone plan over a. Of 2 years using months as a unit of time. Be sure to scale your access by labeling the grid line with some numbers.(pt2 to letter c) what are the labels for the axes of the graph (for x and y)d. is there a proportional relationship between time and the cost of the cell phone plan?Explain how you know!e. Tyler cell phone plan cost $350 to start then there is a $50 charge each month on the same grid as Hans plan in part C above graph the cost of Tyler cell phone plan over Of 2 yearslastly, describe how hans and Tyler's graphs are similar and how they are different..

Answer 1

We know that

• The cost is $200 to start and $50 per month. This can be expressed as follows.

`C=200+50m`

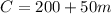
(a) The cost for one month would be

`C=200+50\cdot1=200+50=250`

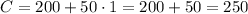
(b) The cost for x months is

`C=200+50x`

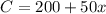
(c) To graph the equation, we use the month as a unit of time, the table values would be

m C

1 250

2 300

3 350

4 400

5 450

6 500

7 550

8 600

9 650

10 700

11 750

12 800

Now, we graph all of these points.

The x-axis label is Months, and the y-axis label is Cost.

(d) The given situation does not show a proportional relationship because a proportional relationship is modeled by the form y = kx, which we do not have in this case.

(e) If the initial fee is $350, the equation is

`C=350+50m`

Let's graph it.

The graphs are similar because they have the same slope but they are different because they have different y-intercepts.