Question

Suppose that you borrow $15,000 for 4 years at 5% toward the purchase of your car. use pmt to find the monthly payments and the total interest for the loan

Answer 1

The formula for the monthly loan payment is given as

`A\text{ = }P((r(1+r)^n)/((1+r)^n-1))`

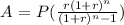
Where

P = loan amount ( initial principal) = $15000

A= Payment amount per period = ?

r = interest rate per period = (5/12) x (1/100) =0.0041667

n = total number of payments or periods = 4 years = 4 x 12 = 48 months

Substituting all these into the above equation gives

`A\text{ =15000( }(0.0041667(1+0.0041667)^(48))/((1+0.0041667)^(48)-1))`
`A\text{ = 15000(}(0.0041667(1.0041667)^(48))/((1.0041667)^(48)-1))`

`\begin{gathered} A\text{ = }15000(\frac{0.0041667\text{ }*1.2208973}{1.2208973\text{ - 1}}) \\ A=\text{ 15000(}(0.005087112781)/(0.2208973)) \end{gathered}`

`\begin{gathered} A=15000(0.023029311) \\ A=\text{ \$345.4396759} \end{gathered}`

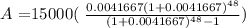
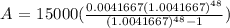
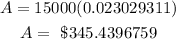
So each month he pays $345.44 to the nearest cent

B)

The total interest for the loan is given by

Total amount paid over the total period of time - Original amount borrowed

Total amount paid over the total period of time = 345.44 x 48 months = $16581.12

The total interest of the loan hence = $16,581.12 - $15,000 = $1,581.12

The total loan interest to the nearest cent = $1,581.12