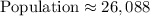Question

The population of a town in Texas is modeled by the function f(x)=16,007(1.031)x. If the initial population (that is, the population when x=0) was measured January 1, 2014, what will the population be on January 1, 2030? Round your answer to the nearest whole number, if necessary.

Answer 1

From the information available, the initial population was 16,007. That figure was taken as at the year zero which is January 1, 2014.

This means

`\begin{gathered} Yr1=2015-2014 \\ Yr2=2016-2014 \\ Yr3=2017-2014 \end{gathered}`

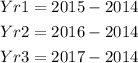
This trend would be used until we get to January 1, 2030, when we would calculate as follows;

`Yr16=2030-2014`

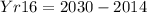
Note that the years count from Jan 1 to Jan 1.

The function that models the yearly growth is;

`f(x)=16007(1.031)^x`

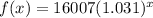
Using the first year, 2014 which is year zero, the result would remain 16,007. That is;

`\begin{gathered} f(0)=16007(1.031)^0 \\ f(0)=16007*1 \end{gathered}`

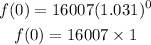
For the 16th year, which is year 2030, we woud now have the following;

`\begin{gathered} f(16)=16007(1.031)^(16) \\ f(16)=16007(1.629816253511204) \\ f(16)=26,088.4687699\ldots \end{gathered}`

Rounded to the nearest whole number, this figure becomes;

ANSWER:

`\text{Population}\approx26,088`