For the first part, we can write
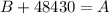
where A is the salary for governor A and B is the salary for governor B.
From the second part, we can write
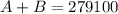
Then, we have 2 equations in 2 unknows.
Solving by substitution method.
If we substitute the firs equation into the second one ,we get
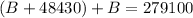
which gives
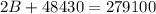
If we move 48430 to the right hand side as -48430, we have

then, B is equal to

Finally, by substituting this result into our first equation, we obtain
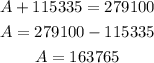
This means that governo A earns $163,765 and gobernor B earns $115,335