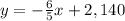Given:
Given data points are (950,100) and (1000,40).
Required:
To find the linear model for this data.
Step-by-step explanation:
The standard form of linear equation is
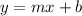
Where
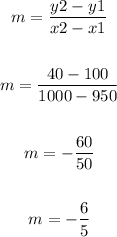
Now
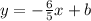
Now we have to find b using the points (950,1000), we get
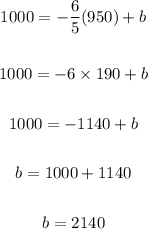
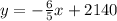
Final Answer: