Question

After how many cakes will their savings be the same for both? b) What will their savings be?

Answer 1

Let "s" represent the amount saved in the bank account and "c" the number of cakes sold.

Jane (J)

Has a starting balance of $70 and she sells "c" cakes for $25 each, you can symbolize the earnings of the cake sales as 25c

You can express the total amount saved using the following expression

`s_J=70+25c`

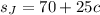
Miriam (M)

Has a starting balance of $100 and shells cakes for $20 each, you can symbolize the total earnings for her cakes sales as 20c

So the total amount saved can be expressed as:

`s_M=100+20c`

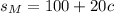
a) To determine how many cakes they must sell so that their savings will be the same, you have to equal both expressions and calculate the value of c:

`\begin{gathered} s_J=s_M \\ 70+25c=100+20c \end{gathered}`

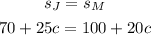
To calculate for c, the first step is to pass the term containing the variable to the left by applying the opposite operation to both sides of the equal sign:

`\begin{gathered} 70+25c-20c=100+20c-20c \\ 70+5c=100 \end{gathered}`

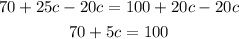
Repeat the process to pass 70 to the right side of the expression

`\begin{gathered} 70-70+5c=100-70 \\ 5c=30 \end{gathered}`

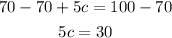
And divide both sides by 5 to reach the value of c

`\begin{gathered} (5c)/(5)=(30)/(5) \\ c=6 \end{gathered}`

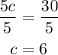
After selling 6 cakes both Jae and Miriam will have saved the same amount.

b)

To determine what will their savings be, you have to replace either one of the expressions with c=6 and calculate for s:

`\begin{gathered} s_J=70+25c \\ s_j=70+25\cdot6 \\ s_j=220 \end{gathered}`

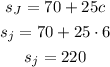
If you solve it using Miriam's expression the result must be the same:

`\begin{gathered} s_M=100+20c \\ s_M=100+20\cdot6 \\ s_M=220 \end{gathered}`

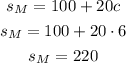
As you see using either equation we arrived to the same result, after selling 6 cakes their total saves will be $220