Given the following parameters
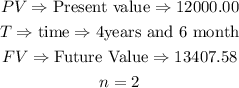
To calculate the nominal rate, we will have to calculate the interest rate and the compounded period, the following formula will be used to find the interest rate and the compounded period.
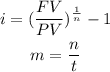
To find the value of the interest, we have
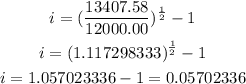
To find the compounded period we will have that
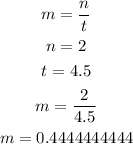
Thus, the nominal rate formula is given as;
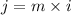
Substitute for m and i to find the nominal rate

The nominal rate in percentage is
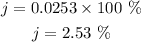
Hence, the nominal rate of the investment if interest is compounded semi-annually is 2.53%