Question

I A family of G holds a ceremony to determine each child's favorite Teenage Mutant Ninja Turtle. The ceremony involves each child's results of choosing 10 numbers out of a hat. If Raphael, Michelangelo, Donatello, and Leonardo are represented with the numbers 1, 2, 3, and 4, respectively, which Teenage Mutant Ninja Turtle would become the favorite of a Child having the following results? Construct a 90% confidence interval estimate of the mean to develop the reasoning for your answer 2 21 4 3 3 3 3 11

Answer 1

Step 1

Write an expression for the mean

`\bar{x}=\text{ }\frac{\sum ^(\square)_{\text{ of terms}}}{\text{mumber of terms}}`
`\begin{gathered} \bar{x}=\frac{2+2+1+\text{ 4 +3+3+3+3}+4+1}{10} \\ \bar{x}=\text{ }(26)/(10) \\ \bar{x}=2.6 \end{gathered}`

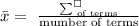
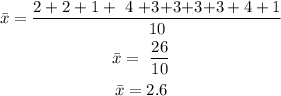
Step 2

Find the standard deviation

`SD=\sqrt[]{\frac{\sum |x-\bar{x}|^2}{n}}`
`SD=\sqrt[]4-2.6`

`\begin{gathered} SD=\sqrt[]{(0.36+0.36+2.56+1.96+0.16+0.16+0.16+0.16+1.96+2.56)/(10)} \\ =\sqrt[]{(10.4)/(10)}\text{ =}\sqrt[]{1.04} \\ =1.02 \end{gathered}`

Find the Z (confidence interval level) value for 90%

`Z_(90)=1.645`

Find the confidence interval

`\begin{gathered} CI=2.6\pm1.645*\frac{1.02}{\sqrt[]{10}} \\ =2.6\pm1.645*0.32 \\ =2.6\pm0.53 \\ \text{Thus,} \\ CI=2.6+0.53\text{ 0r 2.6-0.53} \\ CI=3.13\text{ or 2.07} \end{gathered}`

Hence, a 90% confidence interval estimate of the mean lies between 2 and 3

Therefore, either Michelangelo or Donatello