ANSWER
The equation has one valid solution and one extraneous solution.
A valid solution for x is 5
![\sqrt[]{x-1}-5=x-8](https://img.qammunity.org/2023/formulas/mathematics/college/94fpnoe7ub3e5l1xjbi6pr4mts0jbs42gd.png)
Add 5 to both-side of the equation
![\sqrt[]{x-1}-5+5=x-8+5](https://img.qammunity.org/2023/formulas/mathematics/college/mw1u8t16qmld9putlun8i5oobc73tuxlfp.png)
![\sqrt[]{x-1}=x-3](https://img.qammunity.org/2023/formulas/mathematics/college/vagb0n4xtud3yfidqv7dtmes44iiiteva7.png)
Take the square of both-side
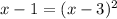
x - 1=x²-6x + 9
Rearrange
x² - 6x + 9 - x + 1 =0
x² - 7x + 10 = 0
We can solve the above quadratic equation using factorization method
x² - 5x - 2x + 10 = 0
x(x-5) - 2(x - 5) = 0
(x-5)(x-2)=0
Either x -5 =0 OR x-2 =0
Either x =5 or x=2
To check whether the equation is valid or non-extraneous, let's plug the values into the equation and see if it gives a true statement
For x =5
![\sqrt[]{5-1}-5=5-8](https://img.qammunity.org/2023/formulas/mathematics/college/atyr8a16pnztnwps2w723wkdqjev7q2q02.png)
![\sqrt[]{4}-5=-3](https://img.qammunity.org/2023/formulas/mathematics/college/v95m5o2m92mxbd69l8iajfiexuxq9slzgt.png)
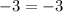
The above is a true statement
For x =2
![\sqrt[]{2-1}-5=2-8](https://img.qammunity.org/2023/formulas/mathematics/college/c25725ueo5ye1k08ateg9v9y1f2lmdzz66.png)
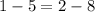
The above is not a true statement
Therefore, the equation has one valid solution and one extraneous solution.
A valid solution for x is 5