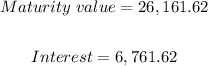Question

Heather invested $19,400 in a growth fund at 3.16% compounded quarterly for 9 years and 6 monthsA) calculate the maturity value of this amount at the end of the termB) Calculate the amount of compounded interest earned

Answer 1

GIVEN:

We are given the details of an investment as follows;

Initial investment = $19,400

Interest rate = 3.16%

Period of investment = 9 years and 6 months

Required;

To use the information given to calculate

(a) The maturity value at the end of the term

(b) The amount of compound interest earned.

Step-by-step solution;

The formula applied in calculating the maturity value is as follows;

`A=P(1+r)^t`

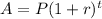
Where the variables are;

`\begin{gathered} A=Maturity\text{ }value \\ \\ P=Initial\text{ }investment\text{ }(19400) \\ \\ r=rate\text{ }of\text{ }interest\text{ }(0.0316) \\ \\ t=time\text{ }in\text{ }years\text{ }(9.5) \end{gathered}`

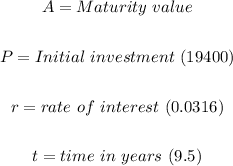
However, for an investment whose interest is compounded at different intervals within 1 year, the formula becomes modified as shown below;

`A=P(1+(r)/(n))^(tn)`

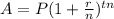
Where the variable n is the number of times interest is compounded annually. For an investment whose interest is compounded quarterly, that is, four times a year, the formula becomes;

`A=P(1+(r)/(4))^(4t)`

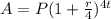
We can now calculate as follows;

`\begin{gathered} A=19400(1+(0.0316)/(4))^(4*9.5) \\ \\ A=19400(1+0.0079)^(38) \\ \\ A=26161.6208681 \\ \\ A\approx26161.62 \end{gathered}`

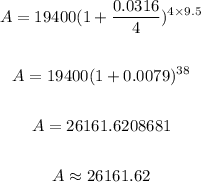
We can now determine the amount of compound interest earned by deducting the initial amount invested from the maturity value. Thus we have;

`\begin{gathered} Interest=A-P \\ \\ Interest=26161.62-19400 \\ \\ Interest=6761.62 \end{gathered}`

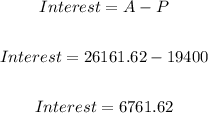
Therefore,

ANSWER:

`\begin{gathered} Maturity\text{ }value=26,161.62 \\ \\ Interest=6,761.62 \end{gathered}`