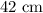Question

Find the radius of a circle on which a central angle measuring 5π/6 radians intercepts an arc on the circle with a length of 35π centimeters.A. 42 cmB. 37 cmC. 61 cmD. 44 cm

Answer 1

the arc lenght s, of a circle of radius r, with central angle θ, is given by the following equation:

`s\text{ = }r\theta`

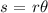
solving for r, we get the following equation:

`r\text{ = }(s)/(\theta)`

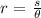
now, replacing in the previous equation the data given in the problem we get:

`r\text{ = }(s)/(\theta)\text{ = }\frac{35\pi}{5\pi\text{ / 6}}\text{ = }\frac{(35\text{ }\pi)\text{ 6 }}{5\pi}\text{ = 42 }`

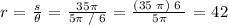
so that, we can conclude that the correct answer is:

`42\text{ cm}`