Question

What volume of O2 at 988 mmHg and 31 °C is required to synthesize 18.5 mol of NO? Express your answer to three significant figures and include the appropriate units.

Answer 1

1) Balance the chemical equation.

`4NH_(3(g))+5O_(2(g))\rightarrow4NO_((g))+6H_2O_((g))`

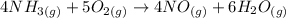
2) Moles of oxygen needed to produce 18.5 mol NO.

The molar ratio between NO and O2 is 4 mol NO: 5 mol O2.

`mol\text{ }O_2=18.5\text{ }mol\text{ }NO*\frac{5\text{ }mol\text{ }O_2}{4\text{ }mol\text{ }NO}=23.125\text{ }mol\text{ }O_2`

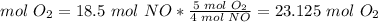
3) Volume of oxygen required.

3.1- List the known and the unknown quantities.

Sample: O2.

Temperature: 31 ºC.

Pressure: 988 mmHg.

Moles: 23.125 mol.

ideal gas constant: 0.082057 L * atm * K^(-1) * mol^(-1)

Volume: unknown

3.2- Set the equation.

`PV=nRT`

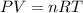
3.3- Converting units.

Temperature: ºC to K.

`K=ºC+273.15`
`K=31\text{ }ºC+273.15=304.15\text{ }K`

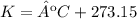
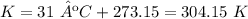
Pressure

760 mmHg = 1 atm.

`atm=988\text{ }mmHg*\frac{1\text{ }atm}{760\text{ }mmHg}=1.3\text{ }atm`

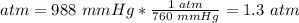
3.4- Plug in the known quantities in the ideal gas equation and solve for V (liters).

`(1.3\text{ }atm)(V)=(23.125\text{ }mol\text{ }O_2)(0.082057\text{ }L*atm*K^(-1)*mol^(-1))(304.15\text{ }K)`
`V=\frac{(23.125molO_2)(0.082057L*atm*K^(-1)*mol^(-1))(304.15K)}{1.3\text{ }atm}`
`V=443.958\text{ }L`

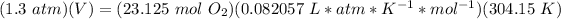
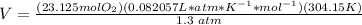
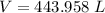
The volume of O2 required is 444 L.