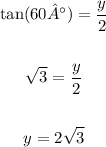In order to calculate the value of x, we can use the cosine relation of the angle 60°.
The cosine is equal to the length of the adjacent leg to the angle over the length of the hypotenuse.
So we have:
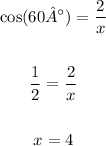
Now, to calculate the value of y, we can use the tangent relation of the angle 60°.
The tangent is equal to the length of the opposite leg to the angle over the length of the adjacent leg to the angle.
So we have: