Identify the domain and range to the following relations and state whether or not the relations are functions. State why or why not the relation is a function.

Question

asked Sep 10, 2023 224k views

1 Answer

Vburojevic · Answer 1 · 2023-09-14T04:23:48+0000

Here, we want to get the range and the domain of the function

The domain refers to the x-values

Looking at the plot, we can see the x-values from 2 to 6

In an interval form, we have this as;

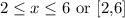
$2\leq x\leq6\text{ or \lbrack{}2,6\rbrack}$

For the range values, we have these as the possible y-values

We can see that the lowest y value is at -4 and the highest y-value is at the point y = 5

So the range is;

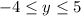
$-4\leq y\leq5$

Now, we want to answer if the relation is a function

For a relation to be a function, no domain value will have 2 range values

But, we can have a single range value having two domain values

As we can see, this rule is correctly followed on the plot and thus, we can confirm that the relation is a function

It is a function because each of the x-values have a single y-value. This means that for every domain value, there is only a range value attached