Answer:
considering the information given, the concentrations at equilbrium are:
CO(g) = 1.30 M
H2O(g) = 1.30 M
CO2(g) = 4.11 M
H2(g) = 4.11 M
Step-by-step explanation:
The question requires us to calculate the concentration of CO, H2O, CO2 and H2, given the following information:
- number of moles of CO = 2.60 mol
- number of moles of H2O = 2.60 mol
- volume of container = 2.00 L
- temperature = 690°C
- equilibrium constant = 10.0
- balanced chemical equation:
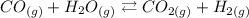
Since the number of moles of CO and H2O were provided, as well as the volume of the container, we can calculate the concentration of this gases in moles per liter:
![\begin{gathered} [CO\rbrack=(2.60mol)/(2.00L)=1.30mol/L=1.30M \\ \\ [H_2O\rbrack=(2.60mol)/(2.00L)=1.30M \end{gathered}]()
Also, since we have the equilibrium constant for this reaction and the concetrations of CO2 and H2 at equilibrium will be the same (they have the same stoichiometric coefficient), we can calculate the concentration of the products using the expression for Keq.
First, let's write the Keq expression for this reaction:
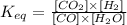
Considering,
[CO2] = [H2] = x
and rearranging this equation to calculate x:
![K_(eq)*[CO\rbrack*[H_2O\rbrack=x^2\rightarrow x=\sqrt[2]{K_(eq)*[CO\rbrack*[H_2O\rbrack}](https://img.qammunity.org/2023/formulas/chemistry/college/m8g68kmwnanoambuteg1l1mbza7zwl6ri0.png)
Now, applying the value of Keq given by the question, and the values of concentration calculated previously, we'll have:
![x=\sqrt[2]{10.0*1.30M*1.30M}\rightarrow x=4.11M^](https://img.qammunity.org/2023/formulas/chemistry/college/md1f8ydv1tf856lop10i5rcf00vqqaja8a.png)
Therefore, considering the information given, the concentrations at equilbrium are:
CO(g) = 1.30 M
H2O(g) = 1.30 M
CO2(g) = 4.11 M
H2(g) = 4.11 M