Explanation:
We have the equation of a quadratic function:
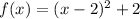
And we need to find and plot the vertex of the equation.
We start by remembering that a quadratic equation is represented by a parabola and that the vertex is the point where the parabola changes direction, usually represented by (h, k) as shown in the following example:
• How do we find the vertex using the given equation?
We find it by comparing our equation with the general vertex form of the quadratic equation:

where
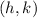
is the vertex, and a is a constant.
Using the given equation, we find the h and k values:
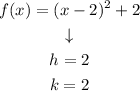
Therefore, the vertex is at (2, 2).
Answer:
The point (2,2) representing the vertex is shown in the image: