The velocity is defined by:
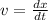
where x is the position of the particle and t is the time.
Plugging the position function given we have that the velocity is:
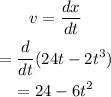
Hence the velocity is given by the function:
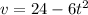
to determine the isntant when the velocity is zero we equate its expression to zero and solve for t:
![\begin{gathered} 24-6t^2=0 \\ 6t^2=24 \\ t^2=(24)/(6) \\ t^2=4 \\ t=\pm\sqrt[]{4} \\ t=\pm2 \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/h59ridw1t09c8j2ypfh4yk62f59ny94cdp.png)
Since time is always positive we conclude that the velocity is zero at t=2 s.
Now that we know at which instant the velocity is zero we need to remember that the acceleration is defined as:
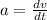
then we have that:
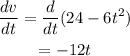
hence the acceleration is:

Plugging the value we found for the time we have that:
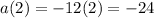
Therefore the acceleration of the particle when its velocity is zero is -24 meters per second per second.