Question

A) Graph the ellipse. Use graph paper or sketch neatly on regular paper. The ellipse must be hand drawn - no computer tools or graphing calculator. Give the center of the ellipse. Give the vertices of the ellipse. Give the endpoints of the minor axis. Give the foci.

Answer 1

The general equation of an ellipse is:

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1.`

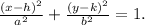
Where:

• (h, k) are the coordinates of the centre,

,

• a and b are the lengths of the legs.

The parts of the ellipse are:

In this case, we have the equation:

`((x+1)^2)/(5^2)+((y-4)^2)/(4^2)=1.`

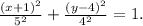
So we have:

• (h, k) = (-1, 4),

,

• a = 5,

,

• b = 4.

A) The graph of the ellipse is:

B) The center of the ellipse is (h, k) = (-1, 4).

C) The vertices of the ellipse are:

• (h + a, k) = (-1 + 5, 4) = ,(4, 4),,

,

• (h - a, k) = (-1 - 5, 4) =, (-6, 4),,

D) The endpoints of the minor axis are:

• (h, k + b) = (-1, 4 + 4 ) = ,(-1, 8),,

,

• (h, k - b) = (-1, 4 - 4) = ,(-1, 0),.

E) To find the focuses, we compute c:

`c=\sqrt[]{a^2-b^2}=\sqrt[]{5^2-4^2}=\sqrt[]{25-16}=\sqrt[]{9}=3.`

The focuses of the ellipse are:

• (h + c, k) = (-1 + 3, 4) = ,(2, 4),,

,

• (h - c, k) = (-1 - 3, 4) = ,(-4, 4),.

Answer

A)

B) (-1, 4)

C) (4, 4), (-6, 4)

D) (-1, 8), (-1, 0)

E) (2, 4), (-4, 4)