How many ways can the letters in the word PARALLEL be arranged?

Question

asked Jan 23, 2023 203k views

1 Answer

Imbolc · Answer 1 · 2023-01-30T09:38:07+0000

Answer:

3,360 ways.

Step-by-step explanation:

In the word PARALLEL

• Number of letters = 8

,

• Number of Ls = 3

,

• Number of As = 2

Since no other restriction is given, the number of ways in which the letters can be arranged is:

We solve to obtain our result.

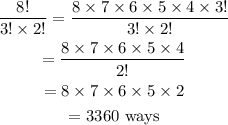
$\begin{gathered} (8!)/(3!*2!)=(8*7*6*5*4*3!)/(3!*2!) \\ =(8*7*6*5*4)/(2!) \\ =8*7*6*5*2 \\ =3360\text{ ways} \end{gathered}$

The word can be arranged in 3,360 ways.