We define the following variables:
• x = cost of one-inch blinders,
,
• y = cost of two-inch blinders.
From the statement of the problem, we know that:
• Rose selected 3 one-inch blinders and 1 two-inch blinder, which cost a total of $23, so we have that:

• Judy selected 5 one-inch blinders and 3 two-inch blinders, which cost a total of $49, so we have that:
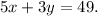
We have the following system of equations:
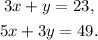
We must solve the system of equations using the elimination method, where you either add or subtract the equations to get an equation in one variable.
1) We multiply the first equation by 3, and we have:
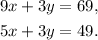
2) Now, we subtract the second equation to the first equation:
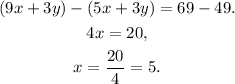
3) Replacing the value x = 5 in the second equation, and solving for y we get:
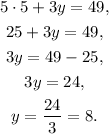
We have found that:

Answer
A one-inch binder costs $5, and a two-inch binder costs $8.