Step-by-step explanation
The area under a curve between two points can be found by doing a definite integral between the two points
Step 1
a) set the intergral
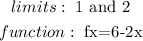
hence
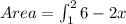
Step 2
evaluate
let ; numbers of intervals
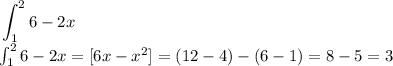
therefore, the area is
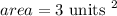
I hope this helps you