The vertex of the given parabola is (h, k)=(0,0).
(x, y)=(2, -4) is a point on the parabola.
The vertex form of a parbola is,
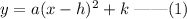
Here, (h, k) is the vertex of parabola.
Put h=0, k=0, x=2 and y=-4 in the above equation.
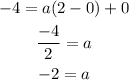
Put a=-2, h=0, k=0 in equation (1) to find the function.
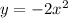
Put y=0 to obtain a quadratic function and solve for x.
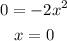
So, there is only one solution to the graph.
Short cut:
Since the parabola touches the x axis when the x intercept is zero, the solution of the quadratic function of the parabola is x=0. So, there is only one solution to the graph.