Question

Find the number of CDs that will produce maximum revenue.

Answer 1

Given data:

Price of CD is,

`p(x)=90-(x)/(6)`

The total revenue is,

`R(x)=90x-(x^2)/(6)`

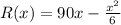
First find the derivative of revenue function and then equate it to zero we have,

`\begin{gathered} R^(\prime)(x)=0 \\ 90-(2x)/(6)=0 \end{gathered}`
`\begin{gathered} (x)/(3)=90 \\ x=90*3 \\ x=270 \end{gathered}`

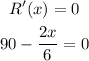
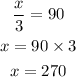
Now, to prove the maximize find the double derivative of revenue function

`\begin{gathered} R^(\doubleprime)(x)<0 \\ (-2)/(6)=(-1)/(3)<0 \end{gathered}`

Thus, 270 CD's will produce maximum revenue.

Answer: Option (c) that is 270.