Step-by-step explanation
From the statement, we have a normal distribution with:
• variable X = time before failure,
,
• mean μ = 42 months,
,
• standard deviation σ = 3 months.
We want to know for how much time the manufacturer will not have more than 9% of the rice cookers returned. So this is equivalent to finding the value x such that the probability of failure is lower than 9%:
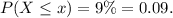
We can compute this probability using the z-scores:
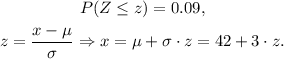
We have the following table for z-scores:
The entries in the table represent the area under the curve, i.e. the probability. We must look for the closest value to the probability of 0.09. From the table, we see that the closest value to this probability is 0.091:
For this value we see that we have the z-score:
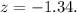
Replacing this value in the equation for x from above, we get:
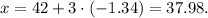
So we have found that for x = 37.98, we have:
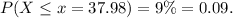
This means that by a time x = 37.98 months, only 9% of the cookers will fail have failed. So the manufacturer must set a warranty period of 38 months to not have more than 9% of the rice cookers returned.
Answer
The manufacturer must set a warranty period of 38 months to not have more than 9% of the rice cookers returned.