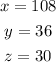Question

Find the measure of each labeled angle as well as the values of x, y, and z.

Answer 1

Notice that the angle labelled as 3y and the angle with a measure of 72° are supplementary angles. Then:

`3y+72=180`

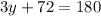
Substract 72 from both sides of the equation:

`\begin{gathered} 3y+72-72=180-72 \\ \Rightarrow3y=108 \end{gathered}`

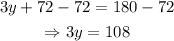
The angle labelled as x and the angle labelled as 3y are corresponding angles. Then, they have the same measure:

`x=3y`

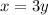
Since 3y=108, then:

`x=108`

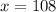
On the equation 3y=108, divide both sides by 3 to find the value of y:

`\begin{gathered} (3y)/(3)=(108)/(3) \\ \Rightarrow y=36 \end{gathered}`

Finally, notice that the angle labelled as 3z+18 and the angle labelled as x are corresponding angles. Then, they have the same measure:

`3z+18=x`

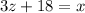
Substitute x=108 and isolate z to find its value:

`\begin{gathered} \Rightarrow3z+18=108 \\ \Rightarrow3z=108-18 \\ \Rightarrow3z=90 \\ \Rightarrow z=(90)/(3) \\ \Rightarrow z=30 \end{gathered}`

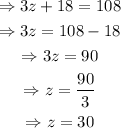
Therefore, the measure of the angles labelled as 3z+18, x and 3y is 108°. The values of x, y and z are:

`\begin{gathered} x=108 \\ y=36 \\ z=30 \end{gathered}`