Question

A penny-farthing is a bicycle with a very large front wheel and a much smaller back wheel. Penny-farthings were popular in the 1800s and were available in different sizes. The ratio of the diameter of the front wheel of a penny-farthing to the diameter of the back wheel is 13:4. What is the ratio of the circumference of the front wheel to the circumference of the back wheel? Explain.

Answer 1

The Solution:

It is given in the question that the ratio of the diameter of the front wheel of a penny-farthing to the diameter of the back wheel is 13:4

`\begin{gathered} (D)/(d)=(13)/(4) \\ \text{Where} \\ D=\text{diameter of the front wheel} \\ d=\text{diameter of the back wheel} \end{gathered}`

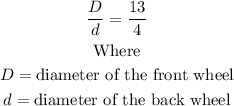
We are required to find the ratio of the circumference of the front wheel to the circumference of the back wheel.

Step 1:

The formula for the circumference of a wheel (that is, a circle) is

`\text{ circumference of a wheel = 2}\pi r=\pi d`

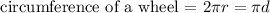
Step 2:

We shall find the ratio of the circumference of the front wheel to the circumference of the back wheel.

`\begin{gathered} (\pi D)/(\pi d)=(13\pi)/(4\pi)=(13)/(4) \\ \text{ So,} \\ 13\colon4 \end{gathered}`

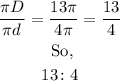
Therefore, the required ratio is 13:4