Question

How do I find which coordinate pairs represent vertices of P'Q'R'S after these two transformations?

Answer 1

We have two transformations.

We will apply them to a generic point P=(x,y), and then we can replace them with any coordinates as inputs.

First transformation: translating 6 units to the right.

This changes the x-coordinate by adding 6 units (x=0 becames x'=6, for example), so we can write:

`P=(x,y)\longrightarrow P^(\prime)=(x+6,y)`

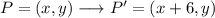
Second transformation: rotate 90 degrees clockwise.

This changes both x and y coordinates. We can look at a drawing to understand the transformation.

The x-coordinate becomes the y-coordinate, and the y-coordinate becomes the negative x-coordinate.

We can then write:

`P^(\prime)=(x+6,y)\longrightarrow P^(\prime)^(\prime)=(y,-x-6)`

So now we know that the final image of a point (x,y) after the two transformations is (y,-x-6).

Then, we can list all four points:

`P=(-3,7)\longrightarrow P^(\prime)^(\prime)=(7,-(-3)-6)=(7,-3)`
`Q=(4,12)\longrightarrow Q^(\prime)^(\prime)=(12,-4-6)=(12,-10)`
`R=(4,-2)\longrightarrow R^(\prime)^(\prime)=(-2,-4-6)=(-2,-10)`
`S=(-3,-7)\longrightarrow S^(\prime)^(\prime)=(-7,-(-3)+6)=(-7,-3)`

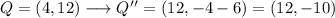
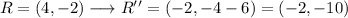
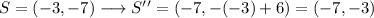
Final coordinates: (7,-3), (12,-10), (-2,-10) and (-7,-3).