Answer:
• z=113°
,
• y=67°
Step-by-step explanation:
In the diagram below, by the principles of vertical and corresponding angles:
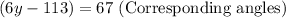
We solve for y:
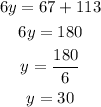
Next, angles z and (6y-113) are on a straight line. Therefore:
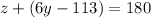
However, recall we stated earlier that (6y-113)°=67°, therefore:
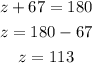
The values of z and y are 113° and 67° respectively.