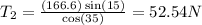We will have the next diagram
Then we can sum the forces in x and sum the forces in y
Forces in x
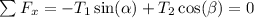
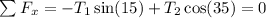
Forces in y
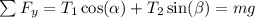
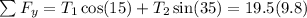
We simplify the equations found and we found the next system of equation
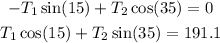
then we isolate the T2 of the first equation
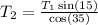
We substitute the equation above in the second equation
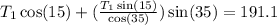
we simplify
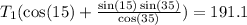
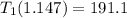
We isolate the T1
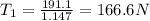
then we can substitute the value we found in T1 in the euation with T2 isolate